Why Spectral GNNs Excel by Discarding High-Frequency

Created in May 10, 2025

2025   ·   GNN   ·   deep-learning

A defining characteristic of spectral Graph Neural Networks (GNNs) [1] is their inherent low-pass filtering mechanism [2], which involves discarding high-frequency signal components, a step that might initially appear ‘arbitrary’ or reductive. This blog explores why this seemingly reductive step of low-pass filtering, which prioritizes the smoother, low-frequency components, proves so beneficial for various node-level and graph-level tasks.

In node-level tasks, such as classifying research areas for papers in a citation network [3], the success of spectral GNNs is largely due to their strong connection with homophily. Homophily defines that connected nodes often share similar features [4]. By attenuating high-frequency variability in attribute signals, these GNNs induce feature smoothing, rendering node representations more uniform across the graph structure, and encouraging similar predictions among locally connected nodes [2].

Additionally, in semi-supervised situations where only a few nodes have labels, a Simple Graph Convolution (SGC)—a type of spectral GNN that acts as a low-pass filter [2]—takes a graph with some labeled nodes as input and generates label predictions for all nodes in the graph [2]. This highlights the effectiveness of spectral GNNs in node-level label propagation under limited supervision.

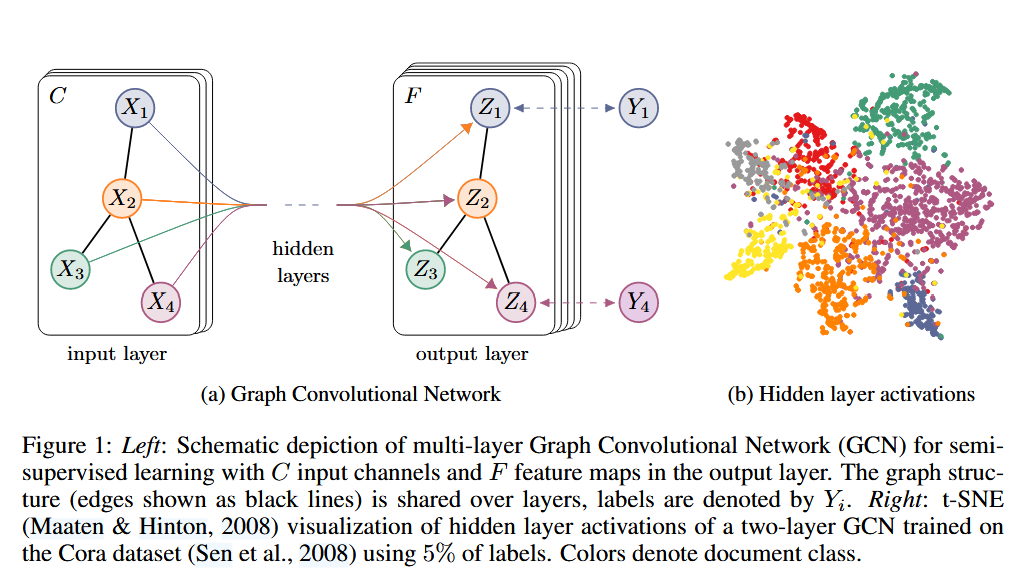Semi-supervised classification with GCNs - hidden layer architecture Figure from source: [3]

For graph-level tasks, such as predicting molecular properties [5] or classifying entire graphs based on their architecture, the primary objective is to derive a representation encapsulating the graph’s global characteristics. By inherently emphasizing low-frequency components, which correspond to smooth variations across the graph [2] and reflect the graph’s underlying global structure [6], spectral GNN captures global patterns.

Furthermore, low-frequency components are often interpreted as the underlying “true signal,” whereas high-frequency elements can represent statistical noise or less relevant local variations [7]. By filtering these out, spectral GNNs provide a cleaner, more robust signal to the subsequent classification model.

However, these benefits are based on certain assumptions. The homophily assumption is critical for node-level tasks; in heterophilic graphs, high-frequency components often carry the discriminative signal, and discarding them is detrimental [3]. Similarly, for tasks like anomaly detection, anomalies might manifest as high-frequency deviations, making these components the signal of interest rather than noise [8].

In conclusion, spectral GNNs’ attenuation of high-frequency signals is a well-founded assumption, not an arbitrary choice, that enhances learning by aligning with data homophily for node-level tasks and global structures for graph-level tasks, thereby prioritizing more robust, smoother signal components. This approach proves highly effective when such data assumptions hold, but it has limitations in heterophilic or anomaly-rich contexts.

References

[1] Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang, and P. S. Yu, “A Comprehensive Survey on Graph Neural Networks,” IEEE Trans. Neural Netw. Learning Syst., vol. 32, no. 1, pp. 4–24, Jan. 2021, doi: 10.1109/TNNLS.2020.2978386.

[2] F. Wu, T. Zhang, A. H. de S. Jr, C. Fifty, T. Yu, and K. Q. Weinberger, “Simplifying Graph Convolutional Networks,” Jun. 20, 2019, arXiv: arXiv:1902.07153. doi: 10.48550/arXiv.1902.07153.

[3] T. N. Kipf and M. Welling, “Semi-Supervised Classification with Graph Convolutional Networks,” Feb. 22, 2017, arXiv:arXiv:1609.02907. doi: 10.48550/arXiv.1609.02907.

[4] O. Platonov, D. Kuznedelev, M. Diskin, A. Babenko, and L. Prokhorenkova, “A critical look at the evaluation of GNNs under heterophily: Are we really making progress?,” Mar. 02, 2024, arXiv: arXiv:2302.11640. doi: 10.48550/arXiv.2302.11640.

[5] O. Wieder et al., “A compact review of molecular property prediction with graph neural networks,” Drug Discovery Today: Technologies, vol. 37, pp. 1–12, Dec. 2020, doi: 10.1016/j.ddtec.2020.11.009.

[6] R. Li, S. Wang, F. Zhu, and J. Huang, “Adaptive Graph Convolutional Neural Networks,” Jan. 10, 2018, arXiv: arXiv:1801.03226. doi: 10.48550/arXiv.1801.03226.

[7] H. NT and T. Maehara, “Revisiting Graph Neural Networks: All We Have is Low-Pass Filters,” May 26, 2019, arXiv: arXiv:1905.09550. doi: 10.48550/arXiv.1905.09550.

[8] S. Li, Y. C. Tan, and T. Vincent, “High-Pass Graph Convolutional Network for Enhanced Anomaly Detection: A Novel Approach”.